HƯỚNG DẪN KHẢO SÁT HÀM SỐ

Các bước khảo sát điều tra và vẽ đồ vật thị hàm số bao gồm các bước chung và các bước khảo gần cạnh và vẽ trang bị thị cho từng các loại đồ thị hàm số gồm đồ thị hàm bậc ba, trang bị thị hàm trùng phương, đồ thị hàm hàng đầu trên bậc nhất

I- SƠ ĐỒ tầm thường KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ.

Bạn đang xem: Hướng dẫn khảo sát hàm số

1. Tập xác định.2. Sự vươn lên là thiên

2.1 Xét chiều biến thiên của hàm số+ Tính đạo hàm y’

+ Tìm những điểm cơ mà tại kia đạo hàm y’ bởi 0 hoặc không xác định

+ Xét vệt đạo hàm y’ với suy ra chiều biến hóa thiên của hàm số.

2.2 Tìm cực trị

2.3 Tìm các giới hạn tại vô rất (), các giới hạn có hiệu quả là vô cực () và tìm tiệm cận nếu như có.

2.4 Lập bảng biến đổi thiên.

Thể hiện không thiếu và chính xác các quý hiếm trên bảng đổi mới thiên.

3. Đồ thị

- Giao của đồ gia dụng thị cùng với trục Oy: x=0 =>y= ? => (0;?)

- Giao của đồ thị với trục Ox: - các điểm CĐ; CT nếu như có.

(Chú ý: trường hợp nghiệm bấm máy tính xách tay được thì OK, nghiệm lẻ giải tay được thì cần giải ra- ví dụ điển hình phương trình bậc 2, còn nghiệm lẽ cơ mà không giải được thì ghi ra giấy nháp cho biết giá trị để khi vẽ cho bao gồm xác- ko ghi vào bài- ví dụ điển hình hàm bậc 3)

- lấy thêm một vài điểm (nếu cần)- (điều này làm sau khoản thời gian hình dung bản thiết kế của thứ thị. Thiếu bên nào học viên lấy điểm phía mặt đó, không rước tùy nhân thể mất thời gian.)

 - nhấn xét về đặc thù của thứ thị. Điều này sẽ ví dụ hơn khi đi vẽ từng đồ dùng thị hàm số.

#Dáng điệu của đồ thị là dáng điệu của bảng biến thiên

II- SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM BẬC BA: y = ax3 + bx2 + cx + d (a khác 0)  .

1. Tập xác định. D=R

2. Sự đổi thay thiên2.1 Xét chiều đổi thay thiên của hàm số

+ Tính đạo hàm:

+ ( Bấm máy tính xách tay nếu nghiệm chẵn, giải trường hợp nghiệm lẻ- không được ghi nghiệm sát đúng)

+ Xét dấu đạo hàm y’ và suy ra chiều vươn lên là thiên của hàm số.

2.2 Tìm cực trị

2.3 Tìm những giới hạn trên vô rất ()

(Hàm bậc tía và những hàm nhiều thức không có TCĐ cùng TCN.)

2.4 Lập bảng biến thiên.

Thể hiện vừa đủ và đúng chuẩn các giá trị trên bảng trở nên thiên.

3. Đồ thị

- Giao của vật dụng thị với trục Oy: x=0 =>y= d => (0; d)

 - Giao của thứ thị với trục Ox:

 - các điểm CĐ; CT trường hợp có.

(Chú ý: giả dụ nghiệm bấm máy vi tính được 3 nghiệm thì OK, còn nếu được một nghiệm nguyên thì phải đưa về tích của một hàm hàng đầu và một hàm bậc hai để giải nghiệm. Trường thích hợp cả tía nghiệm các lẻ thì chỉ ghi ra làm việc giấy nháp để phục vụ cho việc vẽ thứ thị)

- rước thêm một số trong những điểm (nếu cần)- (điều này làm sau khi hình dung mẫu mã của thứ thị. Thiếu bên nào học sinh lấy điểm phía mặt đó, không rước tùy luôn thể mất thời gian.)

- nhận xét về đặc thù của vật thị. Hàm bậc ba nhận điểm  làm trung ương đối xứng.

+ vào đó: x0 là nghiệm của phương trình y’’ = 0 (đạo hàm cung cấp hai bằng 0)

+ Điểm I được call là ‘điểm uốn’ của đồ gia dụng thị hàm số.

=> Các dạng trang bị thị hàm số bậc 3: y = ax3 + bx2 + cx + d (a khác 0)

 

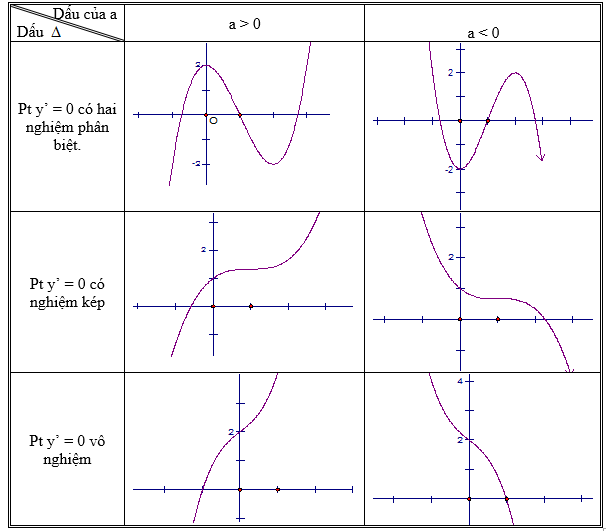
BÀI TẬP LUYỆN VẼ ĐỒ THỊ HÀM SỐ BẬC 3

Khảo liền kề sự đổi thay thiên với vẽ vật thị của những hàm số sau:

 

III. SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐT HÀM SỐ TRÙNG PHƯƠNG y = ax4 + bx2 + c (a khác 0)

IV. SƠ ĐỒ KHẢO SÁT VÀ VẼ ĐT HÀM SỐ y =(ax + b)/(cx+d) - c khác 0, ad- bc không giống 0

Xem cùng tải toàn thể bài này theo liên kết dưới dây

Tải về

Luyện bài bác tập trắc nghiệm môn Toán lớp 12 - xem ngay

Chào mừng các em đã đi vào với bài giảng ngày hôm nay. Hôm nay, họ sẽ được học một phần kiến thức mới, đó là điều tra khảo sát sự trở nên thiên và vẽ đồ gia dụng thị hàm số. Phần kỹ năng này cơ bạn dạng và là căn nguyên để các em học được loài kiến thức nâng cao tới đây với là phần có liên quan đến kỳ thi thpt Quốc gia. Hãy thuộc thacovtc.edu.vn mày mò bài học để không vứt xót ngẫu nhiên kiến thức như thế nào ngay nhé!

Mục tiêu bài bác học điều tra khảo sát sự trở thành thiên với vẽ thiết bị thị hàm số

Sau khi học chấm dứt những bài học kinh nghiệm này, những bạn nhỏ tuổi cần ráng được những kiến thức, kỹ năng sau:

Biết sơ đồ tổng thể để khảo sát điều tra hàm số: search tập xác định, xét chiều thay đổi thiên, tìm cực trị, tìm tiệm cận, lập bảng biến hóa thiên cùng vẽ đồ dùng thị hàm số.Biết giải pháp phân loại những dạng thiết bị thị hàm số.Biết cách điều tra khảo sát và vẽ đồ vật thị của các hàm số bậc ba.Biết giải pháp phân loại các dạng trang bị thị những hàm số trên.

Lý thuyết nên nắm bài khảo sát điều tra sự trở nên thiên và vẽ thứ thị hàm số

Sau đây là những kim chỉ nan trọng chổ chính giữa nhất được itoan biên soạn, giúp các bạn nắm vững bài học và tạo gốc rễ giúp bé bỏng áp dụng giải các bài tập:

I. Sơ đồ khảo sát hàm số

1. Tập xác định

Tìm tập xác định của hàm số.

2. Sự vươn lên là thiênXét chiều đổi thay thiên của hàm số:

+ Tính đạo hàm;

+ Tìm các điểm tại kia đạo hàm bằng 0 hoặc không xác định;

+ Xét vệt đạo hàm và suy ra chiều trở nên thiên của hàm số.

Tìm điểm rất trị.Tìm các giới hạn trên vô cực, những giới hạn vô cực và tra cứu tiệm cận (nếu có).Lập bảng phát triển thành thiên.3. Phụ thuộc vào bảng đổi thay thiên và những yếu tố xác minh ở trên để vẽ vật dụng thị.

Chú ý: 

Nếu hàm số tuần hoàn với chu kì T thì chỉ cần khảo gần cạnh sự biến thiên với vẽ đồ vật thị bên trên một chu kì, tiếp đến tịnh tiến đồ gia dụng thị song song với trục Ox.Nên tính thêm tọa độ một số điểm, đặc biệt là tọa độ những giao điểm của thiết bị thị với những trục.Nên để ý đến tính chẵn, lẻ của hàm số cùng tính đối xứng của đồ vật thị nhằm vẽ cho chính xác.

II. Khảo sát một trong những hàm đơn thức cùng phân thức

1. Hàm số bậc bố y=ax3+bx2+cx+d(a≠0)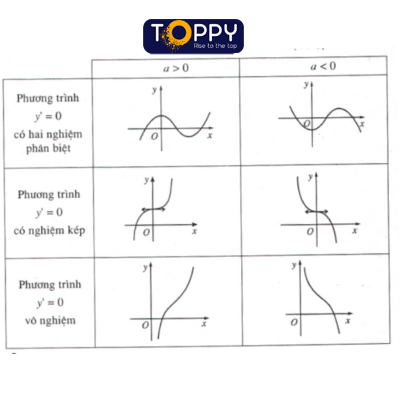

Ví dụ 1: Khảo gần kề sự trở thành thiên và vẽ đồ dùng thị hàm số: y=x3+3x2−4

Giải

(1) Tập xác định: D=R

 (2) Sự trở thành thiên

Chiều trở nên thiên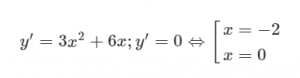

Trên những khoảng (−∞;−2) và (0;+∞) , y′ dương bắt buộc hàm số đồng biến.

Trên khoảng (−2;0) âm phải hàm số nghịch biến.

Cực trị

Hàm số đạt cực đại tại x=−2; y
CD=y(−2)=0

Hàm số đạt cực tiểu tại x=0; y
CT=y(0)=−4

Các số lượng giới hạn tại vô cực

Bảng biến thiên

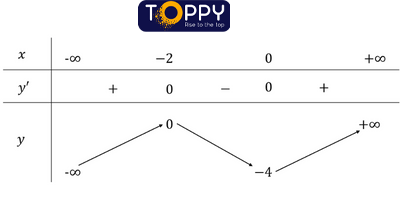
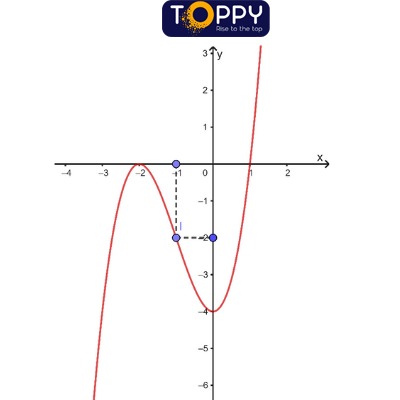
(3) Đồ thị

Ta có: x3+3x2−4=0⇔ x=−2; x=1

Vậy (−2;0) và (1;0) là các giao điểm của đồ gia dụng thị với trục Ox.

Vì y(0)=−4 nên (−4;0) là giao điểm của đồ thị với trục Oy. Điểm kia cũng là điểm cực đái của đồ gia dụng thị.

Chú ý: Đồ thị hàm số vẫn cho tất cả tâm đối xứng là điểm I(−1;−2) . Hoành độ của điểm I là nghiệm của phương trình y′′=0

III. Sự tương giao giữa các đồ thị

1. Giao điểm của hai vật thịGiả sử hàm số y=f(x) có đồ thị là C1 và hàm số y=g(x) có vật thị là C2Để tìm kiếm hoành độ giao điểm của hai vật thị trên là ta giải phương trình f(x)=g(x)Số nghiệm của phương trình trên ngay số giao điểm của hai trang bị thị.2. Sự xúc tiếp của hai tuyến đường congGiả sử hàm số y=f(x) có đồ dùng thị là C1 cùng hàm số y=g(x) có trang bị thị là C2Hai mặt đường cong C1 và C2 tiếp xúc nhau khi và chỉ khi hệ phương trình:

có nghiệm với nghiệm của hệ phương trình bên trên là hoành độ tiếp điểm của hai đường cong đó.

Các chúng ta có thể tham khảo clip hướng dẫn bài học kinh nghiệm dưới đây!

Hướng dẫn giải bài xích tập Khảo gần kề sự biến hóa thiên cùng vẽ đồ dùng thị hàm số

Phần bài tập trong sách giáo khoa rất cạnh bên với kim chỉ nan nên chúng ta cố gắng hoàn thành hết nhé!

Bài 1 trang 43 sách giáo khoa giải tích 12

Khảo ngay cạnh sự vươn lên là thiên cùng vẽ đồ dùng thị của những hàm số bậc cha sau:

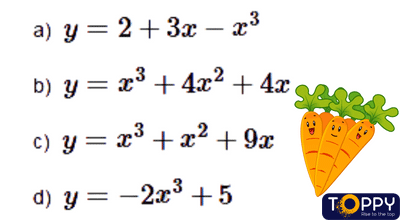
Hướng dẫn giải

a) Tập xác định: R

Sự đổi mới thiên:

Chiều biến đổi thiên: y’ = 3 – 

 ; y’=0  3 –  = 0 x =-1 ( y=4) hoặc x =1 (y =0).

Trên những khoảng (-∞; -1) và (1; +∞), y’ âm đề nghị hàm số nghịch biến. Trên khoảng chừng (-1; 1), y’ dương bắt buộc hàm số đồng biến.

Cực trị:

Hàm đạt cực đại tại x =1 ; yCĐ = y (1) = 4.

Hàm số đạt rất tiểu trên x= 1-; yCT = y(-1) = 0.

Các số lượng giới hạn tại vô cực:

Bảng phát triển thành thiên:

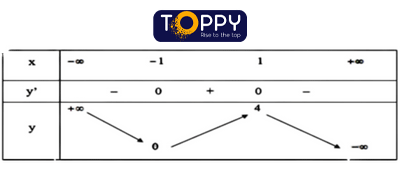
Vậy (-1; 0) và (2; 0) là những giao điểm của đồ dùng thị với trục Ox.

y(0) = 2 cần (0; 2) là giao điểm của vật dụng thị cùng với trục Oy.

b) Tập xác định: R.

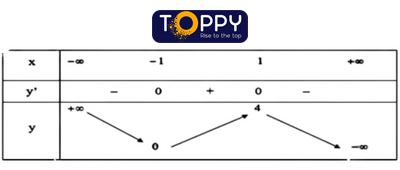
Sự biến thiên:

Chiều thay đổi thiên: y’ = 

 + 8x+4

Cực trị

Bảng đổi mới thiên:

Đồ thị:

Vậy, (0; 0) và (-2; 0) là các giao điểm của thứ thị cùng với trục Ox.

y(0) = 0 bắt buộc (0; 0) là giao điểm của trang bị thị với trục Oy.

Toạ độ một số trong những điểm: (-3; -3); (-1; -1).

c) TXĐ : R

Sự biến thiên:

Chiều trở thành thiên:

Vậy, hàm số đồng biến trên R

Cực trị: Hàm số không có cực trị.

Các số lượng giới hạn tại vô cực:

Bảng trở nên thiên:

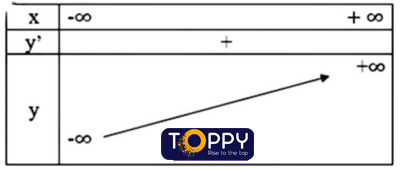
Đồ thị:

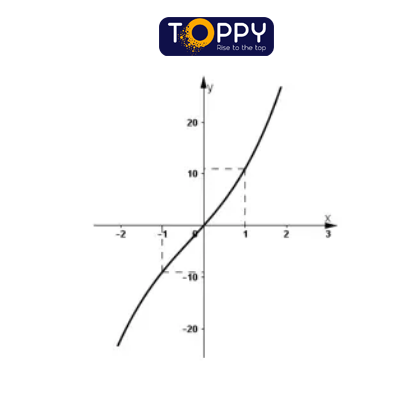
Vậy, (0; 0) là giao điểm của thứ thị cùng với trục Ox.

y(0) = 0 đề xuất (0; 0) là giao điểm của đồ thị với trục Oy.

Đồ thị có tâm đối xứng là vấn đề có hoành độ là nghiệm của phương trình: y” = 0

Bài 2 (trang 43 SGK Giải tích 12)

Khảo cạnh bên tự trở nên thiên và vẽ đồ vật thị của các hàm số bậc tứ sau:

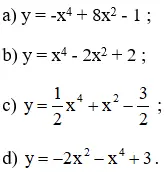
Lời giải:

a) Hàm số y = -x4 + 8x2 – 1.

1) Tập xác định: D = R

2) Sự biến đổi thiên:

+ Chiều biến hóa thiên:

y’ = -4x3 + 16x = -4x(x2 – 4)

y’ = 0 ⇔ -4x(x2 – 4) = 0 ⇔ x = 0 ; x = ±2

Trên khoảng tầm (-∞; -2) cùng (0; 2), y’ > 0 yêu cầu hàm số đồng biến.

Trên các khoảng (-2; 0) cùng (2; +∞), y’ 4 + 8(-x)2 – 1 = -x4 + 8x2 – 1 = y(x)

⇒ Đồ thị thừa nhận Oy làm cho trục đối xứng.

+ Giao với Oy tại điểm (0; -1) (vì y(0) = -1).

+ Đồ thị hàm số đi qua (-3; -10) với (3; 10).

b) Hàm số y = x4 – 2x2 + 2.

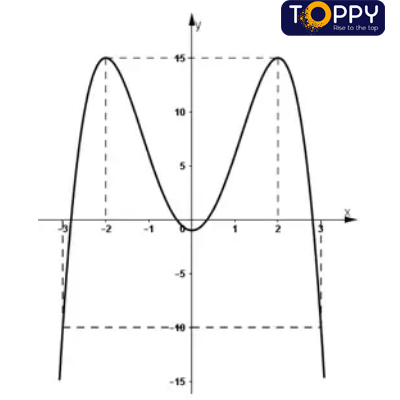
1) Tập xác định: D = R

2) Sự đổi thay thiên:

+ Chiều phát triển thành thiên:

y’ = 4x3 – 4x = 4x(x2 – 1)

y’ = 0 ⇔ 4x(x2 – 1) = 0 ⇔ x = 0 ; x = ±1.

+ Giới hạn:

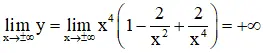
+ Bảng biến đổi thiên:

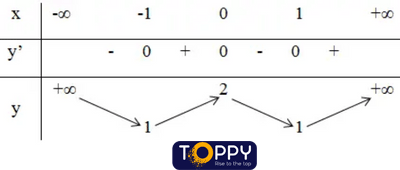
Kết luận :

Hàm số đồng đổi mới trên khoảng chừng (-1; 0) cùng (1; +∞).

Hàm số nghịch biến trên các khoảng (-∞; -1) với (0; 1).

Đồ thị hàm số gồm hai điểm rất tiểu là: (-1; 1) và (1; 1).

Đồ thị hàm số có điểm cực đại là: (0; 2)

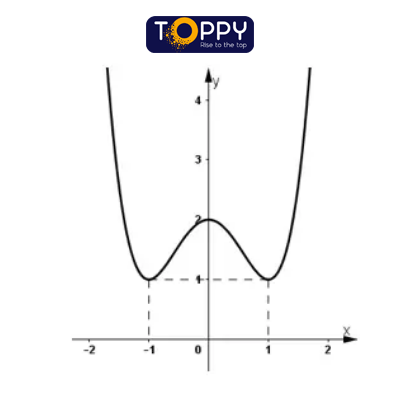
3) Đồ thị:

+ Hàm số chẵn yêu cầu đồ thị hàm số dấn trục Oy là trục đối xứng.

+ Đồ thị hàm số cắt trục tung trên (0; 2).

+ Đồ thị hàm số đi qua (-1; 1) và (1; 1).

+ Đồ thị hàm số:

c) Hàm số 

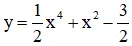
1) Tập xác định: D = R

2) Sự đổi thay thiên:

+ y’ = 2x3 + 2x = 2x(x2 + 1)

y’ = 0 ⇔ 2x(x2 + 1) = 0 ⇔ x = 0

+ Giới hạn:

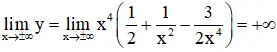
+ Bảng trở nên thiên:

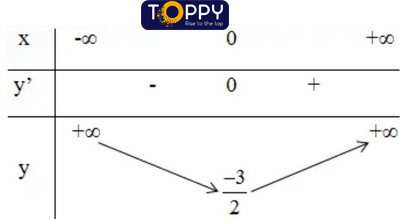
Kết luận: Hàm số đồng biến trên khoảng (0; +∞).

Hàm số nghịch trở nên trên những khoảng (-∞; 0).

Đồ thị hàm số có điểm cực đại là: (0; -3/2).

3) Đồ thị:

+ Hàm số chẵn phải nhận trục Oy là trục đối xứng.

+ Hàm số giảm trục hoành trên điểm (-1; 0) cùng (1; 0).

+ Hàm số cắt trục tung tại điểm 

d) Hàm số y = -2x2 – x4 + 3.

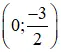
1) Tập xác định: D = R

2) Sự đổi mới thiên:

+ Chiều biến đổi thiên:

y’ = -4x – 4x3 = -4x(1 + x2)

y’ = 0 ⇔ -4x(1 + x2) = 0 ⇔ x = 0

+ Giới hạn:

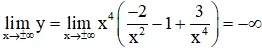
+ Bảng đổi thay thiên:

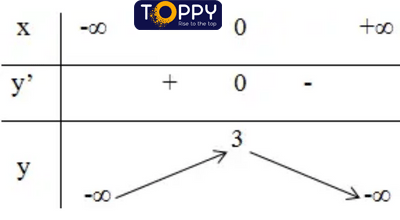
Kết luận: Hàm số đồng phát triển thành trên khoảng (-∞; 0).

Hàm số nghịch biến đổi trên những khoảng (0; +∞).

Đồ thị hàm số tất cả điểm cực to là: (0; 3).

3) Đồ thị:

+ Hàm số là hàm số chẵn cần nhận trục Oy là trục đối xứng.

+ Hàm số giảm trục Ox trên (-1; 0) với (1; 0).

+ Hàm số cắt trục Oy tại (0; 3).

Bài 3 (trang 43 SGK Giải tích 12)

Khảo ngay cạnh sự đổi mới thiên và vẽ vật thị các hàm số phân thức:

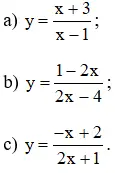
Lời giải:

a) Hàm số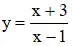 

1) Tập xác định: D = R 1

2) Sự biến đổi thiên:

+ Chiều thay đổi thiên:

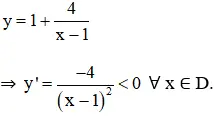
⇒ Hàm số nghịch trở thành trên (-∞; 1) với (1; +∞).

+ cực trị: Hàm số không có cực trị.

+ Tiệm cận:

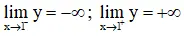
⇒ x = một là tiệm cận đứng.

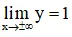
⇒ y = 1 là tiệm cận ngang.

+ Bảng biến hóa thiên:

3) Đồ thị:

+ Giao với Oy: (0; -3)

+ Giao cùng với Ox: (-3; 0)

+ Đồ thị nhấn (1; 1) là trọng điểm đối xứng.

b) Hàm số 

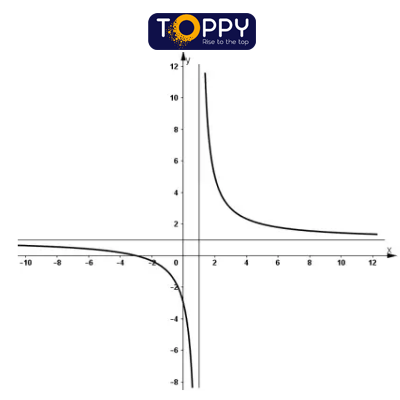
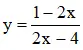
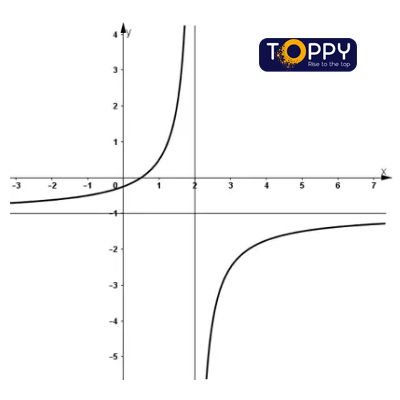
1) Tập xác định: D = R 2

2) Sự biến đổi thiên:

+ Chiều trở nên thiên:

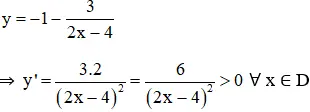
⇒ Hàm số đồng biến hóa trên (-∞; 2) và (2; +∞).

+ cực trị: Hàm số không tồn tại cực trị.

+ Tiệm cận:

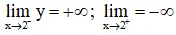
⇒ x = 2 là tiệm cận đứng của vật dụng thị hàm số.

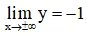
⇒ y = -1 là tiệm cận ngang.

+ Bảng trở thành thiên:

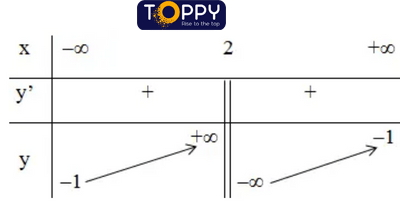
3) Đồ thị:

+ Giao với Oy: (0; -1/4)

+ Giao cùng với Ox: (1/2; 0)

+ Đồ thị hàm số dấn (2; -1) là trọng điểm đối xứng.

số 

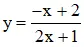
Bài 4 (trang 44 SGK Giải tích 12)

Bằng cách khảo sát hàm số, hãy tra cứu số nghiệm của những phương trình sau:

a) x3 – 3x2 + 5 = 0 ;

b) -2x3 + 3x2 – 2 = 0 ;

c) 2x2 – x4 = -1

Lời giải:

a) Xét y = f(x) = x3 – 3x2 + 5 = 0 (1)

– TXĐ: D = R

– Sự biến thiên:

+ Chiều biến thiên:

f"(x) = 3x2 – 6x = 3x(x – 2)

f"(x) = 0 ⇔ x = 0 ; x = 2

+ Giới hạn:

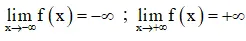
+ Bảng đổi mới thiên:

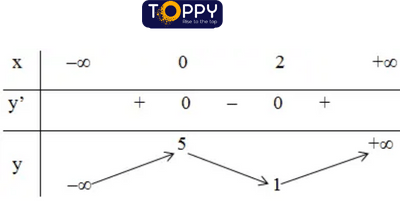
– Đồ thị:

Đồ thị hàm số y = f(x) giảm trục hoành tại một điểm duy nhất.

⇒ phương trình x3 – 3x2 + 5 = 0 chỉ có 1 nghiệm duy nhất.

b) Xét hàm số y = f(x) = -2x3 + 3x2 – 2.

– TXĐ: D = R

– Sự trở thành thiên:

+ Chiều biến thiên:

y’ = -6x2 + 6x = -6x(x – 1)

y’ = 0 ⇔ x = 0 ; x = 1

+ Giới hạn:

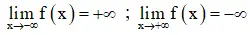
+ Bảng phát triển thành thiên:

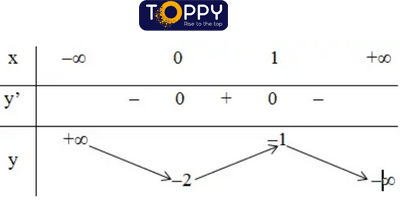
– Đồ thị:

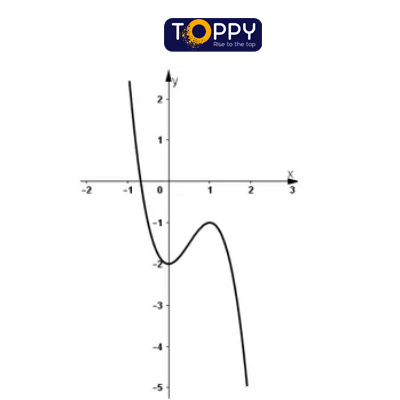
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất

⇒ phương trình f(x) = 0 tất cả nghiệm duy nhất.

Xem thêm: Hướng dẫn chỉnh sửa ảnh đẹp bằng picsart mà có thể mọi người

Vậy phương trình -2x3 + 3x2 – 2 = 0 chỉ tất cả một nghiệm.

Lời kết

Bài học tập ngày hôm nay khá dài nên không ạ? Do bài bác tập đề nghị vẽ và tính toán nên sẽ dài với đói hỏi tính cẩn thận, vì thế các em hãy luyện tập thật nhiều bài xích tập nhằm ghi nhớ, gắng chắc kỹ năng và kiến thức về khảo sát sự vươn lên là thiên với đồ thị hàm số nhé! ngoài ra, các chúng ta có thể truy cập vào website thacovtc.edu.vn. 

thacovtc.edu.vn là doanh nghiệp Edtech về giáo dục đào tạo trực tuyến, cung ứng trải nghiệm học tập tập cá nhân cho hàng trăm ngàn nghìn học sinh, sinh viên với nhà trường nhằm giải đáp phần đông yêu cầu trong câu hỏi học tập thông qua mạng lưới các chuyên viên và giáo viên khắp toàn cầu mà thacovtc.edu.vn gọi là các gia sư học thuật quốc tế. Với kho tàng kiến thức lớn lao theo từng chủ đề, bám sát đít chương trình sách giáo khoa, những thầy cô thacovtc.edu.vn luôn nỗ lực đem đến cho những em những bài bác giảng hay, dễ hiểu nhất, giúp các em tân tiến hơn từng ngày. 

Chúc các bạn sẽ thành công trong việc làm chủ môn Giải tích 11 cùng đạt thật những điểm thưởng.